4.1 Definición de serie.
4.1.1 Finita.
4.1.2 Infinita
4.2 Serie numérica y convergencia. Prueba de razón y raíz.
4.3 Serie de potencias.
4.4 Radio de convergencia.
4.5 Serie de Taylor.
4.6 Representación de funciones mediante serie de Taylor.
4.7 Cálculo de integrales de funciones expresadas como serie de Taylor.
4.1.1 Finita.
4.1.2 Infinita
4.2 Serie numérica y convergencia. Prueba de razón y raíz.
4.3 Serie de potencias.
4.4 Radio de convergencia.
4.5 Serie de Taylor.
4.6 Representación de funciones mediante serie de Taylor.
4.7 Cálculo de integrales de funciones expresadas como serie de Taylor.
4.1 Definición de serie.
SERIES
Una sucesión es un conjunto de términos formados según una ley o regla determinada, por ejemplo:
1, 4, 9, 16, 25
y
1, -x, x^2/2, -x^3/3, x^4/4, -x^5/5
Una serie es la suma indicada de los términos de una sucesión. Así, de las sucesiones anteriores obtenemos las series:
1+4+9+16+25
1 -x + x^2/2 -x^3/3 + x^4/4 -x^5/5
4.1.1 Serie Finita.
Cuando el número de términos es limitado, se dice que la sucesión o serie es finita.
4.1.2 Serie Infinita
Cuando el numero de términos es ilimitado, la sucesión o serie se llama una sucesión infinita o una serie infinita. El término general o termino enésimo es una expresión que indica la ley de formación de los términos. Si la sucesión es infinita, se indica con puntos suspensivos.
Ejemplo:
4.2 Serie numérica y convergencia. Prueba de razón y raíz.
En la serie Sn = u1+u2+u3+...+un, la variable Sn es una función de n. Ahora bien, si hacemos que el número de términos (=n) tienda a infinito, puede ocurrir una de las dos cosas siguientes:
CASO I. Que Sn tienda hacia un límite, digamos u; es decir, que
(1)
lím Sn =u.
n-> x
En este caso se dice que la serie infinita es convergente y que converge al valor u, o que tiene el valor u.
CASO II. Que Sn no tienda hacia ningún limite. En este caso se dice que la serie infinita es divergente.
Ejemplos de series divergentes son
1+2+3+4+5...,
1-1+1-1+...
Como ya hemos dicho, en una serie convergente en el valor de la serie es un número u (llamado a veces la suma) que se define por (1).
A una serie divergente no se le asigna ningún valor.
Criterio de D'Alembert (Criterio de la razón)
Sea una serie  , tal que ak > 0 ( serie de términos positivos).
, tal que ak > 0 ( serie de términos positivos).
 , tal que ak > 0 ( serie de términos positivos).
, tal que ak > 0 ( serie de términos positivos).Si existe
con 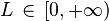 , el Criterio de D'Alembert establece que:
, el Criterio de D'Alembert establece que:
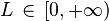 , el Criterio de D'Alembert establece que:
, el Criterio de D'Alembert establece que:- si L < 1, la serie converge.
- si L > 1, entonces la serie diverge.
- si L = 1, no es posible decir algo sobre el comportamiento de la serie.
En este caso, es necesario probar otro criterio, como el criterio de Raabe.
Criterio de Cauchy (raíz enésima)
Sea una serie  , tal que ak > 0 (serie de términos positivos). Y supongamos que existe
, tal que ak > 0 (serie de términos positivos). Y supongamos que existe
 , tal que ak > 0 (serie de términos positivos). Y supongamos que existe
, tal que ak > 0 (serie de términos positivos). Y supongamos que existe![\lim_{k \rightarrow \infty} \sqrt [k] {a_k}=L](http://upload.wikimedia.org/math/9/f/9/9f9c8260d0ee84308bde583dc2ca8991.png) , siendo
, siendo 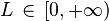
Entonces, si:
- L < 1, la serie es convergente.
- L > 1 entonces la serie es divergente.
- L=1, no podemos concluir nada a priori y tenemos que recurrir al criterio de Raabe, o de comparación, para ver si podemos llegar a alguna conclusión.
4.3 Series de Potencias.
Una serie de potencias alrededor de x=0 es una serie de la forma:
Una serie de potencias alrededor de x=c es una serie de la forma:
En el cual el centro es c, y los coeficientes an son los términos de una sucesión.
4.4 Radio de Convergencia.
Según el teorema de Cauchy-Hadamard, el radio de convergencia de una serie de la forma
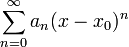 , con
, con 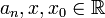 ,
,
viene dado por la expresión:
Limitandonos al conjunto de los números reales, una serie de la forma 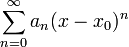 ,
,
con 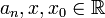 , recibe el nombre de serie de potencias centrada en
, recibe el nombre de serie de potencias centrada en 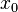 . La serie converge absolutamente para un conjunto de valores de
. La serie converge absolutamente para un conjunto de valores de  que verifica que
que verifica que 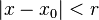 , donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de
, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de  pertenecientes al intervalo
pertenecientes al intervalo 
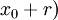 , ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para
, ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para 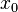 ,
, 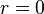 . Si lo hace para cualquier valor de
. Si lo hace para cualquier valor de  ,
, 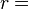
4.5 Serie de Taylor & 4.6 Representación de funciones mediante serie de Taylor.
4.7 Cálculo de integrales de funciones expresadas como serie de Taylor
La función p(x)=a0+a1x+a2x2+..........+anxn, en la que los coeficientes ak son constantes, se llama polinomio de grado n. En particular y=ax+b es un polinomio de primer grado e y=ax2+bx+c es un polinomio de segundo grado. Los polinomios pueden considerarseSi a los polinomios añadimos las funciones de la forma y=p(x)/q(x) (cociente de polinomios, para cuyo cálculo necesitamos también de la división), las funciones raíz cuadrada de x y raíz cúbica de x, y finalmente, las combinaciones aritméticas de los tipos anteriores, obtenemos esencialmente las funciones cuyos valores pueden calcularse por métodos aprendidos en el bachillerato.
A este nivel se tienen nociones de algunas otras funciones tales como log(x), sen(x), ex, ..., pero, aunque se estudian sus propiedades más importantes, no se da una respuesta a las preguntas: ¿Cómo calcularlas? ¿Qué clase de operaciones, por ejemplo, es necesario realizar sobre la x para obtener log(x) o sen(x)?. La respuesta a estas preguntas la proporcionan los métodos desarrollados por el análisis matemático.
Fórmula de Taylor
Sea f(x) una función definida en un intervalo que contiene al punto a, con derivada de todos los órdenes.
El polinomio de primer grado p1(x) = f(a) + f ' (a) (x-a) tiene el mismo valor que f(x) en el punto x=a y también, como se comprueba fácilmente, la misma derivada que f(x) en este punto. Su gráfica es una recta tangente a la gráfica de f(x) en el punto a.
Es posible elegir un polinomio de segundo grado, p2(x) = f(a) + f ' (a) (x-a) + ½ f ' ' (a) (x-a)2, tal que en el punto x=a tenga el mismo valor que f(x) y valores también iguales para su primera y segunda derivadas. Su gráfica en el punto a se acercará a la de f(x) más que la anterior. Es natural esperar que si construimos un polinomio que en x=a tenga las mismas n primeras derivadas que f(x) en el mismo punto, este polinomio se aproximará más a f(x) en los puntos x próximos a a. Así obtenemos la siguiente igualdad aproximada, que es la fórmula de Taylor:f(x) ≈ f(a) + f '(a) (x-a) + (1/2!) f ' '(a) (x-a)2 + ...... + (1/n!) f (n)(a) (x-a) n
El segundo miembro de esta fórmula es un polinomio de grado n en (x-a). Para cada valor de x puede calcularse el valor de este polinomio si se conocen los valores de f(a) y de sus n primeras derivadas.
Para funciones que tienen derivada (n+1)-ésima, el segundo miembro de esta fórmula, como se demuestra fácilmente, difiere del primero en una pequeña cantidad que tiende a cero más rápidamente que (x-a)n. Además, es el único polinomio de grado n que difiere de f(x), para x próximo a a, en un valor que tiende a cero (cuando x tiende a a) más rápidamente que (x-a)n. Si f(x) es un polinomio algebraico de grado n, entonces la igualdad aproximada anterior es una verdadera igualdad.
Para que sea exacta la igualdad aproximada anterior, debemos añadir al segundo miembro un término más, llamado resto:
f(x) = f(a)+f '(a)(x-a)+(1/2!) f ' '(a)(x-a)2+ ...... +(1/n!) f (n)(a)(x-a)n+(1/(n+1)!) f (n+1)(c)(x-a)n+1
El resto tiene la peculiaridad de que la derivada que en él aparece debe calcularse en cada caso, no en el punto a, sino en un punto c convenientemente elegido, desconocido, pero interior al intervalo de extremos a y x.
La demostración de la igualdad anterior es bastante engorrosa, aunque sencilla en esencia.
Las leyes naturales pueden expresarse, por regla general, con buena aproximación por funciones derivables un número arbitrario de veces, y por ello pueden ser aproximadas por polinomios cuyo grado viene determinado por la precisión deseada.
La fórmula de Taylor, que abre el camino para la mayoría de los cálculos en el análisis aplicado, es muy importante desde el punto de vista práctico.
La idea de aproximar una función mediante polinomios o de representarla como suma de un número finito de funciones más sencillas alcanzó un gran desarrollo en el análisis, donde constituye ahora una rama independiente: la teoría de la aproximación de funciones.
Publicado por Arturo Gabriel Torres Sánchez


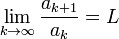

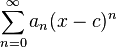
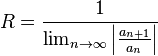


No hay comentarios:
Publicar un comentario